Статьи по темам
Фотогалерея
О значимости параметров ГРВ-грамм жидкофазных объектов
Щевелёв М.И., Фирсов А.А., Баркалов А.В., Ащеулов А.Ю.
2006 г.
Воронежский государственный педагогический университет
Продолжая работу в направлении актуализации применения метода газоразрядной визуализации при исследовании жидкофазных объектов [1, 2, 3], мы столкнулись с проблемой достоверности экспериментальных данных. Очевидно, что водные растворы, которыми является , например, питьевая и техническая вода из различных источников, всегда будут иметь весьма различные составы. Насколько точно можно подметить эти тонкие с макроскопической точки зрения отличия? Решив эту задачу, можно уже смело говорить о преимуществах метода ГРВ, позволяющего проводить с минимальными временными и материально-техническими затратами анализ вод из различных источников.
При успешной обработке газоразрядных изображений капель исследуемых образцов и грамотной интерпретации этих картин, которая, естественно, включает в себя элементы статистики, можно говорить об экспресс-анализе жидких субстанций. В его сути лежит возможность отнести какой-то только взятый образец к тому или иному классу уже исследованных вод. Чем больше в базе данных различных классов и чем меньше отличия между ними, тем у?же должен быть доверительный интервал, определяющий возможность соотнести полученное значение с каким-либо уже имеющимся в нашей базе. Иначе неизбежна ситуация, когда один и тот же образец будет опознан как представитель сразу нескольких классов.
Поскольку все, что мы заведомо знаем об исследуемых образцах, это источники, из которых они получены, то самым разумным будет воспользоваться однофакторным методом статистической обработки, позволяющим сравнивать совокупности значений вновь полученных параметров с определенными контрольными величинами.
Итак, нашей задачей является проверка того, существенны ли различия или совпадения нескольких совокупностей. Воспользуемся для решения поставленной задачи методом однофакторного дисперсионного анализа, который наряду с факторным анализом хорошо подходит для успешного достижения намеченной цели.
Количество уровней намеченного фактора будет, очевидно, равно числу источников (например, числу исследуемых скважин).
Выбор этого метода позволителен, так как выполняются следующие условия: независимо от уровня фактора величины отклика, то есть значения того или иного параметра газоразрядного изображения (ГРИ), имеют нормальный (Гауссовский) закон распределения, а также имеет место гомогенность дисперсий. Даже при небольшом нарушении этих условий наша статистика имеет силу, так как методика дисперсионного анализа является робастной.
В процессе статистической обработки мы проводим разделение дисперсии на части. Вариацию, обусловленную влиянием фактора, положенного нами в основу группировки, характеризует межгрупповая дисперсия ![]() . Она является мерой отклонения частных средних, или средних по группам,
. Она является мерой отклонения частных средних, или средних по группам, ![]() вокруг общей средней
вокруг общей средней ![]()
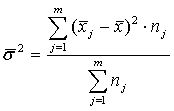 ,
,
где ![]() – число групп;
– число групп; ![]() - число единиц в
- число единиц в ![]() -той группе.
-той группе.
Вариацию, обусловленную влиянием всех прочих факторов, характеризует в каждой группе внутригрупповая дисперсия 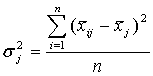 .
.
Учитывая расчет сумм межгруппового и внутригруппового квадратов отклонения и число соответствующих степеней свободы, можем записать выражения для вычисления так называемых средних квадратов, являющихся несмещенными оценками соответствующих дисперсий:
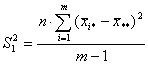 ;
; 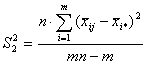 , где звездочка означает усреднение по индексу, который она замещает.
, где звездочка означает усреднение по индексу, который она замещает.
Приведем пример сравнения параметров ГРВ-грамм капель жидкости, полученных с помощью программы «К- drop » [4]. В качестве обрабатываемых параметров в этом случае выбираем три наиболее информативных: площадь свечения ( PS ), общая яркость ( OJ ) и изрезанность ( IZ ). Верхняя строчка соответствует дистиллированной воде, нижняя воде «Бонаква».



|
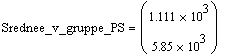
При расчете по аналогии средних в группах общих яркостей и изрезанностей получаем соответственно:  ,
, ![]() .
.
|
|
Общие средние двух других параметров в том же порядке: ![]() ,
, ![]() .
.
Вычисление межгруппового среднего квадрата отклонения.
|
|
|
|
Вычисление внутригруппового среднего квадрата отклонения.
|
|
|
|
Вычисление отношения межгруппового и внутригруппового средних квадратов отклонения.
|
|
|
|

Такая большая разница понятна. Ведь дистиллированная вода не является раствором электролитов. А вот будут ли так же красноречивы результаты сравнения «Бонаквы» с какой-нибудь другой минеральной водой? Возьмем в качестве последней минеральную воду «Икорецкая».


В этом случае отношение средних квадратов отклонений уже не такое впечатляющее, однако, и этого более чем достаточно. Конечно, при систематизации большого объема данных мы не сможем ограничиться визуальной оценкой подобных результатов. Для этого мы будем использовать F -критерий Фишера-Снедекора, который определим как критический при определенном уровне значимости ![]() , при числе степеней свободы
, при числе степеней свободы ![]() ,
, ![]() . Тогда F -распределение Фишера-Снедекора будет иметь следующую функцию плотности:
. Тогда F -распределение Фишера-Снедекора будет иметь следующую функцию плотности:
![]()
где Г – гамма-функция.
Литература:
- Баркалов А.В., Щевелев М.И., Ащеулов А.Ю. Использование метода ГРВ для анализа химического состава питьевых вод. /Международный Конгресс по биоэлектрографии /Тезисы – Спб., 2004.
- Фирсов А.А., Щевелев М.И., Ащеулов А.Ю. Регистрация изменения структурно-термодинамических характеристик воды при различных температурах методом газоразрядной визуализации. /Международный Конгресс по биоэлектрографии /Тезисы – Спб., 2005.
- Фирсов А.А., Щевелев М.И., Ащеулов А.Ю. Использование процесса ГРВ при определении влияния различных растворителей на структурные особенности воды. /Международный Конгресс по биоэлектрографии /Тезисы – Спб., 2005.
- Кащей Г.Б. Щевелев М.И., Баркалов А.В., Ащеулов А.Ю. Новое программное обеспечение для обработки кирлиановских изображений. /Международный Конгресс по биоэлектрографии /Тезисы – Спб., 2000.
- Войдите или зарегистрируйтесь, чтобы получить возможность отправлять комментарии





 Нанотехнологии в водоочистке: достижения отечественной науки на службе здоровья.
Нанотехнологии в водоочистке: достижения отечественной науки на службе здоровья.
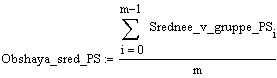
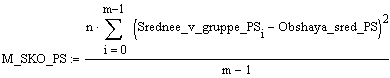
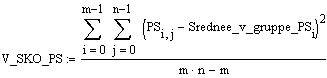
 Фильтры для воды "Геракл" с графеновым сорбентом: полный каталог и прайс-лист.
Фильтры для воды "Геракл" с графеновым сорбентом: полный каталог и прайс-лист.